Contents

Семинар

Теорема Гаусса-Маркова.

Теорема. Если

  1. \(y = X\beta + u\), \(\beta\) – константы.

  2. Оценивается регрессия \(\hat{y} = X\hat{\beta}\) при помощи МНК.

  3. Матрица \(X\) детерминирована и имеет полный ранг.

  4. \(\mathbb{E}(u) = 0, \mathrm{Var}(u) = \sigma^2 I\).

  5. \(n >> k\),

то

  1. \(\hat{\beta}\) существуют и единственны.

  2. \(\hat{\beta}\) линейны по \(y\).

  3. \(\mathbb{E}(\hat{\beta}) = \beta\).

  4. \(\hat{\beta}\) эффективны в классе линейных по \(y\) несмещённых оценок.

Гетероскедастичность.

Определение.

Нарушение предпосылки ТГМ: \(\mathrm{Var}(u_i) = \sigma_i^2 \ne \sigma\).

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

# Статистика
import statsmodels.formula.api as smf # Модели и гипотезы
import statsmodels.stats.api as sms # Тесты

x = np.arange(50)
u = [np.random.normal(0, i) for i in range(50)]
y = 3 + 2 * x + u

plt.scatter(x, y)
plt.plot(x, y - u, c='r')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Гетероскедастичность')

Text(0.5, 1.0, 'Гетероскедастичность')
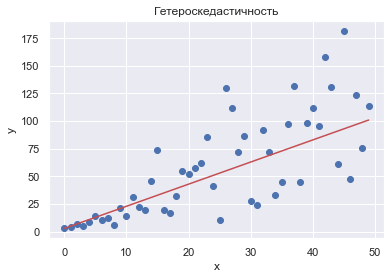
../../_images/seminar_7_1.png

Проблема: \(\hat{\sigma}^2 = \dfrac{RSS}{n-k}\) неверна, а значит неверны \(\mathrm{se}(\hat{\beta})\), а значит неверно строятся доверительные интервалы и нельзя доверять результатам проверки гипотез.

Идентификация.

Существует большое количество различных статистических тестов. Например:

  1. Goldfeld-Quandt test.

Тестируется гипотеза \(H_0\) против \(H_1\): $\( \begin{cases} H_0: \sigma_i^2 = \sigma^2, \\ H_1: \sigma_i \sim X_j. \end{cases} \)$

Схема:

  1. Отсортировать регрессор \(X_j\) по возрастанию.

  2. Разбить отсортированный ряд на три одинаковые части. Предполагается, что первая часть имеет случайную ошибку \(\sigma^2_1\), а третья часть \(\sigma^2_2\). Вторая часть выбрасывается.

  3. Проверить гипотезу $\( \begin{cases} H_0: \sigma_1^2 = \sigma_2^2, \\ H_1: \sigma_1^2 \ne \sigma_2^2. \end{cases} \)$

Для этого оцениваем модель по первой части наблюдений и получаем \(RSS_1\), оцениваем по второй части наблюдений и получаем \(RSS_2\), а затем используем \(F\)-статистику:

\[ F = \dfrac{RSS_2 / (n_2 - k)}{RSS_1 / (n_1 - k)}. \]

Если \(H_0\) отвергается, то в данных наблюдается гетероскедастичность из-за \(X_j\).

data.shape[0] / 3 - 6 # F_{17974, 17974}

17974.0

data = sns.load_dataset('diamonds')
data.head()
carat cut color clarity depth table price x y z
0 0.23 Ideal E SI2 61.5 55.0 326 3.95 3.98 2.43
1 0.21 Premium E SI1 59.8 61.0 326 3.89 3.84 2.31
2 0.23 Good E VS1 56.9 65.0 327 4.05 4.07 2.31
3 0.29 Premium I VS2 62.4 58.0 334 4.20 4.23 2.63
4 0.31 Good J SI2 63.3 58.0 335 4.34 4.35 2.75 
model = smf.ols('np.log(price) ~ depth + table + x + y + z', data = data).fit()

model.summary()
OLS Regression Results
Dep. Variable: np.log(price) R-squared: 0.919
Model: OLS Adj. R-squared: 0.919
Method: Least Squares F-statistic: 1.226e+05
Date: Thu, 12 Nov 2020 Prob (F-statistic): 0.00
Time: 00:07:49 Log-Likelihood: -9493.6
No. Observations: 53940 AIC: 1.900e+04
Df Residuals: 53934 BIC: 1.905e+04
Df Model: 5
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 2.8430 0.079 35.811 0.000 2.687 2.999
depth 0.0093 0.001 8.986 0.000 0.007 0.011
table -0.0109 0.001 -18.413 0.000 -0.012 -0.010
x 0.7973 0.007 118.034 0.000 0.784 0.811
y 0.0365 0.005 7.425 0.000 0.027 0.046
z 0.0615 0.009 7.204 0.000 0.045 0.078
Omnibus: 24199.104 Durbin-Watson: 1.346
Prob(Omnibus): 0.000 Jarque-Bera (JB): 2130668.668
Skew: 1.252 Prob(JB): 0.00
Kurtosis: 33.688 Cond. No. 5.43e+03


Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 5.43e+03. This might indicate that there are
strong multicollinearity or other numerical problems.
?sms.het_goldfeldquandt

# GQ-test: the first value is F-stat
sms.het_goldfeldquandt(model.model.endog, model.model.exog)
# H0 не отвергается, гетероскедастичность не выявлена

(0.5571425675792742, 0.9999999999999999, 'increasing')

  1. Breush-Pagan test.

Тестируется гипотеза \(H_0\) против \(H_1\):

\[\begin{split} \begin{cases} H_0: \sigma_i^2 = \sigma^2, \\ H_1: \sigma_i^2 \sim f(Z\alpha), \end{cases} \end{split}\]

где \(f\) – некоторая гладкая функция, \(Z\) – некоторые регрессоры, которые могут быть и не включены в нашу модель.

Схема:

  1. Оценить регрессию \(\hat{y} = X\hat{\beta}\).

  2. Получить оценку \(\hat{\sigma}^2 = \dfrac{RSS}{n}\) (смещённая).

  3. Создать новую переменную \(q := \dfrac{y-\hat{y}}{\hat{\sigma}^2}\) (поэлементно).

  4. Оценить регрессию \(\hat{q} = Z\hat{\alpha}\).

  5. Протестировать \(H_0\) при помощи статистики $\( \chi^2 = \dfrac{ESS}{2} \sim \chi^2_{\text{число регрессоров в \)Z\(, не считая константный}}. \)$

?sms.het_breuschpagan

# Первое значение -- значение статистики
sms.het_breuschpagan(model.resid, model.model.exog)
# H0 отвергается, гетероскедастичность выявлена

(318.88832638372446,
 8.68231926481354e-67,
 64.14981882459652,
 5.505510514064581e-67)

  1. White test.

Тестируется гипотеза \(H_0\) против \(H_1\):

\[\begin{split} \begin{cases} H_0: \sigma_i^2 = \sigma^2, \\ H_1: \exists i: \sigma_i^2 \ne \sigma^2, \end{cases} \end{split}\]

Схема:

  1. Оценить регрессию \(\hat{y} = X\hat{\beta}\).

  2. Оценить регрессию \((y_i - \hat{y}_i)^2 = a_0 + \sum_jb_jX_j + \sum_jc_jX_j^2 + \sum_{i<j}d_jX_iX_j\). Найти \(R^2\) в этой регрессии.

  3. Проверить \(H_0\) при помощи статистики \(\chi^2 = n \times R^2 \sim \chi^2_{1 + j + j + (j^2 - j)/2}\).

?sms.het_white

# Первое значение -- значение статистики
sms.het_white(model.resid, model.model.exog)
# H0 отвергается, гетероскедастичность выявлена

(8939.302502210943, 0.0, 535.5453119814345, 0.0)

Корректировка гетероскедастичности.

I. В теории: пусть знаем \(\sigma_i^2\) для всех \(i\). В этом случае мы можем “исправить” модель так, чтобы гетероскедастичности не было.

Задание 1. Рассмотрим модель \(y_i = \beta_0 + \beta_1x_i + u_i\), \(\mathrm{Var}(u_i) = \dfrac{\sigma^2}{(3 + x_i)^2}\). Скорректируйте гетероскедастичность в модели и выпишите выражение для оценок скорректированной модели.

Решение. Заметим, что дисперсия случайной ошибки представляется в виде \(\mathrm{Var}(u_i) = \sigma^2 \times f(x_i).\) Поделим каждый компонент регрессии на \(\sqrt{f(x_i)}\):

\[ (3 + x_i)y_i = \beta_0(3+x_i) + \beta_1x_i(3+x_i) + (3+x_i)u_i. \]

Переобозначим: \((3 + x_i)y_i =: \tilde{y}_i\), \(\beta_0(3+x_i) =: \beta_0\tilde{X}_{1i}\), \(\beta_1x_i(3+x_i) =: \beta_1\tilde{X}_{2i}\), \((3+x_i)u_i =: \tilde{u}_i\). Заметим, что в модели

\[ \tilde{y}_i = \beta_0\tilde{X}_{1i} + \beta_1\tilde{X}_{2i} + \tilde{u}_i \]

гетероскедастичности нет, потому что

\[ \mathrm{Var}(\tilde{u}_i) = \dfrac{(3 + x_i)^2\sigma^2}{(3 + x_i)^2} = \sigma^2, \]

а значит, к ней применима ТГМ. Оценки в этой модели можно рассчитать по стандартной формуле:

\[ \hat{\beta} = (\tilde{X}'\tilde{X})^{-1}\tilde{X}'\tilde{y}. \]

Задание 2. Рассмотрим модель \(y = X\beta + u\), \(\mathrm{Var}(u) = \sigma^2A\), \(A\) известна.

  1. Скорректируйте гетероскедастичность в модели и выпишите выражение для оценок этой модели.

  2. Выведите дисперсию оценок скорректированной модели.

  3. Выведите дисперсию оценок МНК.

Решение.

  1. Как и в предыдущей задаче, корректировка производится делением компонентов модели на корень из функции, стоящей при \(\sigma\). В матричном случае эта операция превращается в домножение на \(A^{-1/2}\), где

\[\begin{split} A^{-1/2} = P \begin{pmatrix} 1/\sqrt{\lambda_1} & 0 & \ldots & 0 \\ 0 & 1/\sqrt{\lambda_1} & \ldots & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 1/\sqrt{\lambda_n} \end{pmatrix}P^{-1}, \end{split}\]

где \(P\) – матрица собственных векторов.

Скорректированная модель:

\[ A^{-1/2}y = A^{-1/2}X\beta + A^{-1/2}u \]
\[ \hat{\beta}^{\mathrm{corr}} = (\tilde{X}'\tilde{X})^{-1}\tilde{X}'\tilde{y} = (X'A^{-1/2}A^{-1/2}X)^{-1}X'A^{-1/2}A^{-1/2}y = (X'A^{-1}X)^{-1}X'A^{-1}y. \]
\[ \mathrm{Var}(\hat{\beta}^{\mathrm{corr}}) = (X'A^{-1}X)^{-1}X'A^{-1}\sigma^2A A^{-1}X(X'A^{-1}X)^{-1} = (X'A^{-1}X)^{-1}\sigma^2. \]

Заметим, что

\[ \mathrm{Var}(\hat{\beta}^{\mathrm{corr}}) = (X'A^{-1}X)^{-1}\sigma^2 = (\tilde{X}'\tilde{X})^{-1}\sigma^2. \]
\[ \mathrm{Var}(\hat{\beta}^{\mathrm{OLS}}) = \mathrm{Var}((X'X)^{-1}X'y) = (X'X)^{-1}X'AX(X'X)^{-1}\sigma^2. \]

II. На практике: \(\sigma_i^2\) не знаем. Тогда есть три варианта.

Вариант 1: исправить только доверительные инетрвалы для параметров модели, оцениваемой при помощи МНК,так, чтобы они были устойчивы к гетероскедастичности. Тогда

\[ \hat{\mathrm{Var}}(\hat{\beta}_{OLS})_{HC} = (X'X)^{-1}X'\hat{\mathrm{Var}}(u)_{HC}X(X'X)^{-1}. \]

\(\hat{\mathrm{Var}}(u)_{HC}\) можно взять разными способами:

  1. \(HC_0\): \(\hat{\mathrm{Var}}(u)_{HC_0} = \mathrm{diag}(\hat{u}^2_1, \ldots, \hat{u}^2_n)\).

  2. \(HC_3\): \(\hat{\mathrm{Var}}(u)_{HC_3} = \mathrm{diag}(\hat{u}^2_{1, CV}, \ldots, \hat{u}^2_{n, CV})\).

Задание 3. Рассмотрим модель \(y_i = \beta x_i + u_i\). Известно, что \(y_1 = y_2 = y_3 = 2\), \(x_1 = x_2 = 1\), \(x_3 = 4\).

  1. Найдите \(\hat{\beta}_{OLS}\).

  2. Найдите \(\hat{\mathrm{Var}}(\hat{\beta_{OLS}})_{HC_0}\).

  3. Найдите \(\hat{\mathrm{Var}}(\hat{\beta_{OLS}})_{HC_3}\).

Решение.

  1. Вспомним, что в модели парной регрессии без константы МНК-оценка коэффициента строится следующим образом:

\[ \hat{\beta}_{OLS} = \dfrac{\sum_i x_iy_i}{\sum x_i^2} = \dfrac{12}{18} = \dfrac{2}{3}. \]

  1. Найдём остатки:

\[ \hat{y} = x\hat{\beta} = \begin{pmatrix} 2/3 & 2/3 & 8/3 \end{pmatrix}'. \]
\[ \hat{u} = y - \hat{y} = \begin{pmatrix} 4/3 & 4/3 & -2/3 \end{pmatrix}' \]

Тогда

\[\begin{split} \hat{\mathrm{Var}}(\hat{\beta_{OLS}})_{HC_0} = \dfrac{1}{18} \begin{pmatrix} 1 & 1 & 4 \end{pmatrix} \begin{pmatrix} (4/3)^2 & 0 & 0 \\ 0 & (4/3)^2 & 0 \\ 0 & 0 & (-2/3)^2 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 4 \end{pmatrix}\dfrac{1}{18}. \end{split}\]

  1. Чтобы получить остатки на кросс-валидации, нужно для \(i\)-го наблюдения оценить модель на прочих \(n-1\) наблюдениях и рассчитать остатки по полученным оценкам. Для нашего примера:

\(y_i\)

\(x_i\)

\(\hat{\beta}_{CV}\)

\(\hat{y}_{CV}\)

\(\hat{u}_{CV}\)

2

1

\(\frac{10}{17}\)

\(\frac{10}{17}\)

\(\frac{24}{17}\)

2

1

\(\frac{10}{17}\)

\(\frac{10}{17}\)

\(\frac{24}{17}\)

2

4

2

8

-6

Тогда

\[\begin{split} \hat{\mathrm{Var}}(\hat{\beta_{OLS}})_{HC_3} = \dfrac{1}{18} \begin{pmatrix} 1 & 1 & 4 \end{pmatrix} \begin{pmatrix} (24/17)^2 & 0 & 0 \\ 0 & (24/17)^2 & 0 \\ 0 & 0 & (-6)^2 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \\ 4 \end{pmatrix}\dfrac{1}{18}. \end{split}\]
model.cov_params()
Intercept depth table x y z
Intercept 0.006303 -7.520541e-05 -2.917492e-05 -1.201055e-04 -3.607090e-05 2.583795e-04
depth -0.000075 1.077368e-06 1.561260e-07 2.118084e-06 4.742715e-07 -4.281410e-06
table -0.000029 1.561260e-07 3.530415e-07 -2.831128e-07 1.047273e-07 7.671272e-08
x -0.000120 2.118084e-06 -2.831128e-07 4.562656e-05 -2.053421e-05 -3.904137e-05
y -0.000036 4.742715e-07 1.047273e-07 -2.053421e-05 2.417944e-05 -5.709749e-06
z 0.000258 -4.281410e-06 7.671272e-08 -3.904137e-05 -5.709749e-06 7.293067e-05 
model.cov_HC0

array([[ 2.53646463e-02, -3.79811138e-04, -3.70015534e-05,
        -1.64932777e-03, -1.37831330e-03,  4.96374117e-03],
       [-3.79811138e-04,  6.02318499e-06,  1.90578318e-07,
         3.32326293e-05,  1.65964402e-05, -8.15647500e-05],
       [-3.70015534e-05,  1.90578318e-07,  4.89255718e-07,
        -6.41399781e-06,  5.51885356e-06,  6.46117971e-07],
       [-1.64932777e-03,  3.32326293e-05, -6.41399781e-06,
         1.70474508e-03, -1.30321102e-03, -6.59553761e-04],
       [-1.37831330e-03,  1.65964402e-05,  5.51885356e-06,
        -1.30321102e-03,  1.42545309e-03, -1.88329799e-04],
       [ 4.96374117e-03, -8.15647500e-05,  6.46117971e-07,
        -6.59553761e-04, -1.88329799e-04,  1.38362462e-03]])

model.HC0_se

Intercept    0.159263
depth        0.002454
table        0.000699
x            0.041289
y            0.037755
z            0.037197
dtype: float64

# Модель можно переоценить с учётом робастных стандартных ошибок
model_hc = smf.ols('np.log(price) ~ depth + table + x + y + z', data = data).fit(cov_type = 'HC0')
model_hc.summary()
OLS Regression Results
Dep. Variable: np.log(price) R-squared: 0.919
Model: OLS Adj. R-squared: 0.919
Method: Least Squares F-statistic: 4.141e+04
Date: Thu, 12 Nov 2020 Prob (F-statistic): 0.00
Time: 00:37:09 Log-Likelihood: -9493.6
No. Observations: 53940 AIC: 1.900e+04
Df Residuals: 53934 BIC: 1.905e+04
Df Model: 5
Covariance Type: HC0
coef std err z P>|z| [0.025 0.975]
Intercept 2.8430 0.159 17.851 0.000 2.531 3.155
depth 0.0093 0.002 3.800 0.000 0.005 0.014
table -0.0109 0.001 -15.642 0.000 -0.012 -0.010
x 0.7973 0.041 19.310 0.000 0.716 0.878
y 0.0365 0.038 0.967 0.334 -0.037 0.111
z 0.0615 0.037 1.654 0.098 -0.011 0.134
Omnibus: 24199.104 Durbin-Watson: 1.346
Prob(Omnibus): 0.000 Jarque-Bera (JB): 2130668.668
Skew: 1.252 Prob(JB): 0.00
Kurtosis: 33.688 Cond. No. 5.43e+03


Warnings:
[1] Standard Errors are heteroscedasticity robust (HC0)
[2] The condition number is large, 5.43e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

Вариант 2. Использовать FGLS.

\[ \hat{\beta}_{FGLS} = (X'\hat{\Omega}^{-1}X)^{-1}X'\hat{\Omega}^{-1}y \]

\(\hat{\Omega}\) можно оценивать по-разному: Пример 1, Пример 2, Пример 3, Пример 4. Можно использовать итерационный алгоритм, описанный, например, в Википедии.

Метод полезен, когда у нас есть некоторое представление о том, как устроена ковариационная матрица случайных ошибок.

from statsmodels.regression.linear_model import OLS, GLS

# Например, как описано в примере 3
log_resid = np.log(model.resid ** 2)
hat_omega_model = OLS(log_resid, model.model.exog).fit()
weights = 1 / np.exp(model.model.exog @ hat_omega_model.params)

weights

array([71.38203285, 90.7696654 , 99.93012519, ..., 59.07510695,
       49.6225778 , 47.19220893])

model_gls = GLS(model.model.endog, model.model.exog, sigma = weights).fit()
model_gls.summary()
GLS Regression Results
Dep. Variable: y R-squared: 0.918
Model: GLS Adj. R-squared: 0.918
Method: Least Squares F-statistic: 1.212e+05
Date: Thu, 12 Nov 2020 Prob (F-statistic): 0.00
Time: 00:43:41 Log-Likelihood: -11563.
No. Observations: 53940 AIC: 2.314e+04
Df Residuals: 53934 BIC: 2.319e+04
Df Model: 5
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 2.9610 0.075 39.314 0.000 2.813 3.109
x1 0.0104 0.001 11.192 0.000 0.009 0.012
x2 -0.0118 0.001 -18.941 0.000 -0.013 -0.011
x3 0.8470 0.002 475.091 0.000 0.844 0.851
x4 -0.0076 0.000 -25.813 0.000 -0.008 -0.007
x5 0.0142 0.002 5.840 0.000 0.009 0.019
Omnibus: 7143.461 Durbin-Watson: 1.381
Prob(Omnibus): 0.000 Jarque-Bera (JB): 93702.657
Skew: -0.047 Prob(JB): 0.00
Kurtosis: 9.456 Cond. No. 5.05e+03


Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 5.05e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

III. Использовать бутстрэп.

Pairs Bootstrap.

Разные реализации, например, так.

\[ \hat{\mathrm{Var}}(\hat{\beta})^* = \dfrac{1}{B-1}\sum_{j = 1}^B(\hat{\beta}_j^* - \bar{\beta}_j^*)(\hat{\beta}_j^* - \bar{\beta}_j^*)^T. \]
from statsmodels.api import OLS
n_reps = 100
coef_matr = np.zeros((n_reps, 6))

for i in range(n_reps):
    # 1. Строим бутстрэп-выборку
    random_inds = np.random.randint(0, len(model.model.endog), size = len(model.model.endog))
    y_b = model.model.endog[random_inds]
    X_b = model.model.exog[random_inds, :]
    
    # 2. Оцениваем модель и сохраняем оценки
    model_b = OLS(y_b, X_b).fit()
    coefs = np.array(model_b.params).reshape(1, -1)
    coef_matr[i, :] = coefs
    
# Центрируем оценку каждого коэффициента
coef_matr = coef_matr - np.mean(coef_matr, axis = 0)

# Собираем ковариационную матрицу
cov_matr = 0
for i in range(n_reps):
    cov_matr += coef_matr[i, :].reshape(-1, 1) @ coef_matr[i, :].reshape(-1, 1).T

pd.DataFrame(cov_matr / (n_reps - 1), columns = model.model.exog_names, index = model.model.exog_names)
Intercept depth table x y z
Intercept 0.099790 -0.001459 -0.000153 0.024355 -0.037759 0.021478
depth -0.001459 0.000022 0.000001 -0.000211 0.000421 -0.000338
table -0.000153 0.000001 0.000001 -0.000170 0.000176 -0.000009
x 0.024355 -0.000211 -0.000170 0.042448 -0.043042 0.000539
y -0.037759 0.000421 0.000176 -0.043042 0.045780 -0.003994
z 0.021478 -0.000338 -0.000009 0.000539 -0.003994 0.005586 
model.cov_params()
Intercept depth table x y z
Intercept 0.006303 -7.520541e-05 -2.917492e-05 -1.201055e-04 -3.607090e-05 2.583795e-04
depth -0.000075 1.077368e-06 1.561260e-07 2.118084e-06 4.742715e-07 -4.281410e-06
table -0.000029 1.561260e-07 3.530415e-07 -2.831128e-07 1.047273e-07 7.671272e-08
x -0.000120 2.118084e-06 -2.831128e-07 4.562656e-05 -2.053421e-05 -3.904137e-05
y -0.000036 4.742715e-07 1.047273e-07 -2.053421e-05 2.417944e-05 -5.709749e-06
z 0.000258 -4.281410e-06 7.671272e-08 -3.904137e-05 -5.709749e-06 7.293067e-05

Wild Bootstrap.

(Этот метод нужно будет реализовать в домашнем задании самостоятельно).

Семинар Семинар