Семинар¶

Постановка задачи.¶

Сначала вспомним постановку задачи. Как и в предыдущих задачах, мы хотим максимизировать логарифм функции правдоподобия $\ell(x | \theta)$, чтобы найти оценку вектора параметров $\theta$. Однако бывает так, что эта функция имеет такой вид, что максимизировать сложно (например, если под логарифмом оказывается сумма). Идея EM-алгоритма состоит в том, чтобы ввести латентные переменные $z$ и использовать совместное распределение $p(X, Z)$ для нахождения $\hat{\theta}$.

EM-алгоритм в общем виде.¶

Инициализация: задать начальные условия на $\theta_{old}$.

E.1-шаг: найти условное распределение латентных переменных $p(Z | X, \theta_{old})$.

E.2-шаг: построить функцию $Q(\theta, \theta_{old}) = E_{Z | X, \theta}(\ell(x, z | \theta) | x, \theta_{old})$.

M-шаг: максимизировать $Q$ по $\theta$.

Далее повторять E- и M-шаги до сходимости.

Обоснование EM-алгоритма.¶

Для обоснования ЕМ-алгоритма и понимания обозначений рассмотрим пример:

Пусть $X_1, X_2, \ldots, X_n$ $\sim f(x, | \theta)$, где $f$ – какая-то функция плотности, $\theta$ – вектор неизвестных параметров этой плотности.

Пусть латентные переменные принимают всего два значения: $Z \in \{0, 1\}$ – с вероятностями $P(Z = 0) = p_1$, $P(Z = 1) = 1-p_1$.

Тогда $\ell(x | \theta) = \sum_i \ln f(x_i | \theta)$.

Заметим, что

\[ \ell(x | \theta) = \sum_i \ln f(x_i | \theta) = \sum_i \sum_j P(Z = j)\ln f(x_i | \theta) = \sum_i \sum_j P(Z = j)\ln \dfrac{f(x_i, Z = j | \theta)}{P(Z = j | x_i, \theta)} = \]

(чтобы понять последний переход, распишите знаменатель выражения под логарифмом по формуле условной вероятности)

\[ = \sum_i \sum_j P(Z = j)\ln \dfrac{f(x_i, Z = j | \theta) P(Z = j)}{P(Z = j | x_i, \theta)P(Z = j)} = \]

\[ = \sum_i \sum_j P(Z = j) \ln \dfrac{f(x_i, Z = j | \theta)}{P(Z = j)} + \sum_i \sum_j P(Z = j) \ln \dfrac{P(Z = j)}{P(Z = j | x_i, \theta)} = \]

\[ M(P(Z = j), \theta) + D_{KL}[P(Z = j) || P(Z = j | x_i, \theta)]. \]

Так как $D_{KL} \ge 0$, то $M(P(Z = j), \theta)$ является нижней оценкой на логарифм правдоподобия. Идея EM-алгоритма состоит в том, чтобы поочерёдно максимизировать $M(P(Z = j), \theta)$ по $P(Z = j)$ (на E-шаге) и по $\theta$ (на M-шаге).

E-шаг.

Максимизируем $M(P(Z = j), \theta)$ по $P(Z = j)$.

Так как $\ell(x | \theta)$ не зависит от $P(Z = j)$, то максимум $M(P(Z = j), \theta)$ по $P(Z = j)$ будет достигнут, когда $D_{KL}$ минимальна.

Минимальная $D_{KL}(A || B)$ равна 0, и это достигается, когда $A || B$. Из этого делаем вывод, что на E-шаге мы устанавливаем

\[ P(Z = j) := P(Z = j | x_i, \theta^{old}). \]

M-шаг.

Максимизируем $M(P(Z = j), \theta)$ по $\theta$. Распишем $M$ ещё раз:

\[ M = \sum_i \sum_j P(Z = j) \ln \dfrac{f(x_i, Z = j | \theta)}{P(Z = j)} \]

Заметим, что знаменатель подлогарифмического выражения не зависит от $\theta$. Выбросим его и заменим $P(Z = j)$ на результат, полученный нами на E-шаге:

\[ M = \sum_i \sum_j P(Z = j | x_i, \theta^{old}) \ln f(x_i, Z = j | \theta) = \sum_i E_{Z | x_i, \theta_{old}}(\ln f(x_i, Z = j | \theta)) := Q(\theta | \theta^{old}). \]

Далее мы максимизируем $Q$ по по $\theta$, обновляем $\theta$ на аргмаксимум $Q$, и возвращаемся к E-шагу.

Обозначения.¶

Теперь соотнесём обозначения из общей постановки EM-алгоритма с теми, что мы получили в примере.

$p(Z)$ – это безусловное распределение $Z$. По сути, это массив размера $1\times k$, где $k$ – число значений $Z$.

$p(Z | X, \theta_{old})$ – это условное распределение $Z$ при условии выборки. По сути, это массив размера $N\times k$, где $N$ – размер выборки, $k$ – число значений $Z$. Каждая строчка есть вектор вероятностей того, что на данном наблюдении $Z$ равно соответствующему значению.

$E_{Z | X, \theta}(\cdot)$ – это сумма матожиданий $\sum_i E_{Z | x_i, \theta}$ по всем наблюдениям выборки.

$p(\cdot)$ – распределение того, что стоит в скобках. Эта функция может оказаться функцией вероятности или функцией плотности в зависимости от контекста.

Пример с лекции: задача о кластеризации (разделение смеси нормальных распределений).¶

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(123)
y1 = np.random.normal(0, 1, 100)
y2 = np.random.normal(4, 1, 100)
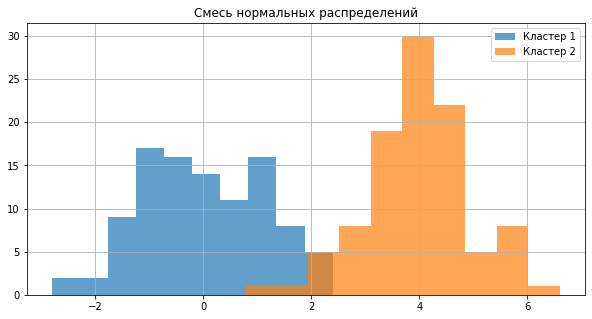
plt.figure(figsize = (10, 5))
_ = plt.hist(y1, alpha = 0.7, label = 'Кластер 1')
_ = plt.hist(y2, alpha = 0.7, label = 'Кластер 2')
_ = plt.legend()
_ = plt.title("Смесь нормальных распределений")
_ = plt.grid()

x = np.concatenate((y1, y2))
x.shape

(200,)

Постановка задачи.¶

Пусть мы точно знаем, что наблюдения принадлежат одному из двух кластеров. Пусть в первом кластере наблюдения берутся из нормального $\mathcal{N}(\mu_1, \sigma_1^2)$ распределения, а во втором – из нормального $\mathcal{N}(\mu_2, \sigma_2^2)$ распределения. Предположим, что все наблюдения независимы, и вероятность того, что наблюдение относится к первому кластеру, равна $p_1$.

# Определите вектор параметров для данной задачи и задайте начальные условия
# theta = (mu_1, sigma2_1, mu2, sigma2_2, p_1)
# (воспользовались эвристикой)
theta = np.array([np.min(x), (np.max(x) - np.min(x)) / 2, np.max(x), (np.max(x) - np.min(x)) / 2, 1/2])
theta

array([-2.79858911,  4.69844652,  6.59830393,  4.69844652,  0.5       ])

Определение латентных переменных.¶

$z \in \{1, 2\}$ – номер кластера.

Вспомним, что у нас есть обозначение $p_1 = P(z = 1)$ – вероятность отнести наблюдение к первому кластеру.

E1-шаг.¶

Найти условное распределение латентных переменных $p(Z | X, \theta_{old})$. Для данной задачи это означает, что мы должны получить массив $200\times2$ (200 наблюдений, 2 значения $z$). Нам достаточно найти только один столбец массива – этот столбец будет размера $200\times1$ (то есть вероятность того, что $z = 1$) – потому что второй столбец определяется однозначно как ($1 - $ первый столбец).

По формуле условной вероятности: $$ p(z | x, \theta_{old}) = \dfrac{p(z, x | \theta_{old})}{p(x | \theta_{old})} $$

и $$ p(x | z, \theta_{old}) = \dfrac{p(x, z | \theta_{old})}{p(z)} $$

Тогда $$ P(z_i = 1 | x_i, \theta_{old}) = \dfrac{p(z_i = 1, x_i | \theta_{old})}{f(x_i | \theta_{old})} $$

\[ = \dfrac{f(x_i | z_i = 1, \theta_{old})p_1}{p_1f(x_i | z_i = 1, \theta_{old}) + (1-p_1)f(x_i | z_i = 2, \theta_{old})} \]

# Задайте плотность x
def f(x, mu, sigma2):
    return 1 / np.sqrt(2 * np.pi * sigma2) * np.exp(-1/2 * 1/sigma2 * (x - mu)**2)

# Рассчитайте распределение латентных переменных на наших данных
p_z_1 = f(x, mu = theta[0], sigma2 = theta[1]) * theta[4] / (theta[4] * f(x, mu = theta[0], sigma2 = theta[1]) + 
                                                       (1-theta[4]) * f(x, mu = theta[2], sigma2 = theta[3]))

# Заметим, что полученный массив имеет размер 200x1
p_z_1.shape

(200,)

E2-шаг.¶

Постройте функцию $Q(\theta | \theta_{old}) = E_{Z | X, \theta}(\ell(x, z | \theta) | x, \theta_{old})$.

По формуле условной вероятности: $$ p(x, z | \theta) = p(x | \theta, z) \times p(z) $$

\[ Q(\theta | \theta_{old}) = \sum_i P(z_i = 1 | x, \theta_{old})[\ln f(x_i | \theta) + \ln p_1] + (1 - P(z_i = 1 | x, \theta_{old})[\ln f(x_i | \theta) + \ln(1-p_1)]. \]

M-шаг.¶

Выведите формулы для максимизации $Q$.

\[ Q'_{\mu_1} = \sum_i P(z_i = 1 | x, \theta_{old}) \dfrac{(x_i - \mu_1)}{\sigma_1^2} \]

\[ \mu_1^{new} = \dfrac{\sum_i P(z_i = 1 | x, \theta_{old}) x_i}{\sum_i P(z_i = 1 | x, \theta_{old})} \]

Аналогично,

\[ \mu_2^{new} = \dfrac{\sum_i (1 - P(z_i = 1 | x, \theta_{old})) x_i}{\sum_i (1 - P(z_i = 1 | x, \theta_{old}))} \]

Далее:

\[ Q'_{\sigma_1^2} = \sum_i P(z_i = 1 | x, \theta_{old}) (-\dfrac{1}{2\sigma^2_1} + \dfrac{1}{2}\dfrac{(x_i - \mu)^2}{\sigma_1^4}) \]

\[ \sigma_1^{2, new} = \dfrac{\sum_i (x_i - \mu)^2 P(z_i = 1 | x, \theta_{old})}{\sum_i P(z_i = 1 | x, \theta_{old})} \]

Аналогично для $\sigma_2^{2, new}$.

Далее:

\[ Q'_{p_1} = \sum_i P(z_i = 1 | x, \theta_{old}) \dfrac{1}{p_1} - (1 - P(z_i = 1 | x, \theta_{old})) \dfrac{1}{1 - p_1} \]

\[ p_1^{new} = \dfrac{\sum_i P(z_i = 1 | x, \theta_{old})}{n} \]

# Реализуйте формулы для одного M-шага
mu_1 = np.sum(p_z_1 * x) / np.sum(p_z_1)

mu_2 = np.sum((1-p_z_1) * x) / np.sum(1-p_z_1)

sigma2_1 = np.sum((x - mu_1) ** 2 * p_z_1)/ np.sum(p_z_1)

sigma2_2 = np.sum((x - mu_2) ** 2 * (1 - p_z_1))/ np.sum(1 - p_z_1)

p1 = np.sum(p_z_1) / len(x)

theta_new = np.array([mu_1, sigma2_1, mu_2, sigma2_2, p1])

theta

array([-2.79858911,  4.69844652,  6.59830393,  4.69844652,  0.5       ])

theta_new

array([0.01920326, 1.45048155, 3.83743546, 1.30562653, 0.48023499])

Решение задачи кластеризации.¶

На каждом шаге будем дополнительно рассчитывать значение $Q$. Для этого определим дополнительные функции:

# Логарифм функции плотности x
def lnf(x, mu, sigma2):
    return -1/2 * np.log(2 * np.pi * sigma2) - 1/2 * (x - mu) ** 2 / sigma2

def Q_f(x, theta, p_z_1):
    ell1 = lnf(x, theta[0], theta[1]) + np.log(theta[4])
    ell2 = lnf(x, theta[2], theta[3]) + np.log(1 - theta[4])
    return np.sum(p_z_1 * ell1 + (1 - p_z_1) * ell2)

Соберём E- и М-шаги в функцию.

def EM(x, theta):
    
    Q_history = []
    
    for i in range(100):
        
        # E-step
        p_z_1 = f(x, mu = theta[0], sigma2 = theta[1]) * theta[4] / (theta[4] * f(x, mu = theta[0], sigma2 = theta[1]) + 
                                                       (1-theta[4]) * f(x, mu = theta[2], sigma2 = theta[3]))
        
        # M-step
        mu_1 = np.sum(p_z_1 * x) / np.sum(p_z_1)
        mu_2 = np.sum((1-p_z_1) * x) / np.sum(1-p_z_1)
        sigma2_1 = np.sum((x - mu_1) ** 2 * p_z_1)/ np.sum(p_z_1)
        sigma2_2 = np.sum((x - mu_2) ** 2 * (1-p_z_1))/ np.sum(1 - p_z_1)
        p1 = np.sum(p_z_1) / len(x)
        theta_new = np.array([mu_1, sigma2_1, mu_2, sigma2_2, p1])
        
        theta = theta_new
        
        Q_history.append(Q_f(x, theta, p_z_1))
        
        if len(Q_history) > 1:
            if np.linalg.norm(Q_history[-1] - Q_history[-2]) < 1e-8:
                break
        
    return theta, Q_history

# Реинициализируем для удобства
np.random.seed(123)
y1 = np.random.normal(0, 1, 100)
y2 = np.random.normal(4, 1, 100)
x = np.concatenate((y1, y2))
theta = np.array([np.min(x), (np.max(x) - np.min(x)) / 2, np.max(x), (np.max(x) - np.min(x)) / 2, 1/2])

theta, Q = EM(x, theta)

# Вспомним, что theta = (mu1, sigma2_1, mu2, sigma2_2, p1)
theta

array([0.1335007 , 1.45409172, 4.09054136, 0.72902767, 0.52735233])

fig, ax = plt.subplots(1, 2, figsize = (15, 7))
ax[0].plot(Q, label = 'Q')
ax[0].legend()
ax[0].grid()
ax[0].set_xlabel("Итерация")
ax[0].set_ylabel("Q")
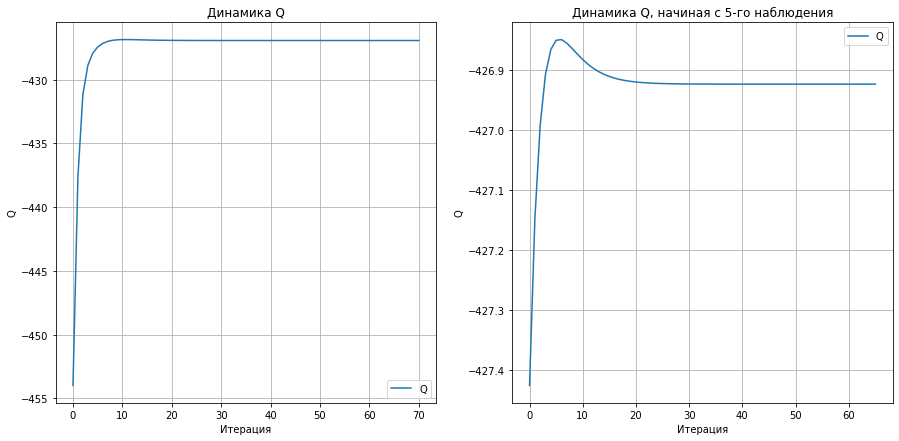
_ = ax[0].set_title("Динамика Q")
ax[1].plot(Q[5:], label = 'Q')
ax[1].legend()
ax[1].grid()
ax[1].set_xlabel("Итерация")
ax[1].set_ylabel("Q")
_ = ax[1].set_title("Динамика Q, начиная с 5-го наблюдения")

Динамика Q.¶

Во многих источниках утверждается, что на каждой итерации EM-алгоритма значение неполного правдоподобия не уменьшается. Доказывается это следующим образом.

\[ \ell(x | \theta_{new}) = M(\theta_{new} | \theta_{old}) + D_{KL} \ge M(\theta_{new} | \theta_{old}) \ge M(\theta_{old} | \theta_{old}) = \ell(x | \theta_{old}) \]

Последнее равенство верно, потому что после E-шага значение неполного правдоподобия совпадает с его нижней оценкой.

Заметим, однако, что мы можем сделать вывод только о неполном правдоподобии

\[ M(\theta_{new} | \theta_{old}) \ge M(\theta_{old} | \theta_{old}), \]

но не об ожидаемом неполном правдподобии

\[ M(\theta_{old} | \theta_{old}) \text{ ? } M(\theta_{old} | \theta_{old-1}), \]

то есть мы ничего не можем сказать о соотношениях нижней оценки на правдоподобие, если используются значения $P(Z = j)$ до и после E-шага. Можно заметить, что из этого следует, что мы также не можем сравнить

\[ M(\theta_{new} | \theta_{old}) \text{ ? } M(\theta_{old} | \theta_{old-1}). \]

На практике это означает, что динамика $Q$ может оказаться не монотонной, что мы и увидели в примере выше (другими словами это описано здесь).

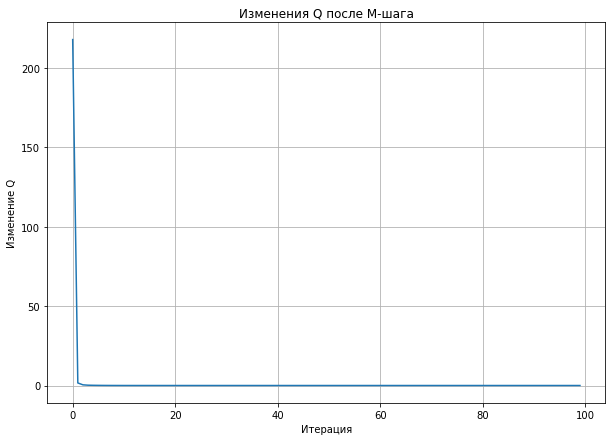
Заметим, что динамика изменения $Q$ до и после M-шага обязана быть монотонной в соответствии с доказательством выше.

def EM_dynamics(x, theta):
    
    Q_M = []
    
    for i in range(100):
        
        # E-step
        p_z_1 = f(x, mu = theta[0], sigma2 = theta[1]) * theta[4] / (theta[4] * f(x, mu = theta[0], sigma2 = theta[1]) + 
                                                       (1-theta[4]) * f(x, mu = theta[2], sigma2 = theta[3]))
        
        # Рассчитаем Q до M-шага
        Q_0 = Q_f(x, theta, p_z_1)
        
        # M-step
        mu_1 = np.sum(p_z_1 * x) / np.sum(p_z_1)
        mu_2 = np.sum((1-p_z_1) * x) / np.sum(1-p_z_1)
        sigma2_1 = np.sum((x - mu_1) ** 2 * p_z_1)/ np.sum(p_z_1)
        sigma2_2 = np.sum((x - mu_2) ** 2 * (1-p_z_1))/ np.sum(1 - p_z_1)
        p1 = np.sum(p_z_1) / len(x)
        theta_new = np.array([mu_1, sigma2_1, mu_2, sigma2_2, p1])
        
        theta = theta_new
        
        # Рассчитаем Q после M-шага и сохраним разницу
        Q_M.append(Q_f(x, theta, p_z_1) - Q_0)
        
    return theta, Q_M

# Реинициализируем для удобства
np.random.seed(123)
y1 = np.random.normal(0, 1, 100)
y2 = np.random.normal(4, 1, 100)
x = np.concatenate((y1, y2))
theta = np.array([np.min(x), (np.max(x) - np.min(x)) / 2, np.max(x), (np.max(x) - np.min(x)) / 2, 1/2])

theta, Q_M = EM_dynamics(x, theta)

# Вспомним, что theta = (mu1, sigma2_1, mu2, sigma2_2, p1)
theta

array([0.1335007 , 1.45409173, 4.09054136, 0.72902766, 0.52735233])

plt.figure(figsize = (10, 7))
plt.plot(Q_M)
plt.title("Изменения Q после M-шага")
plt.xlabel("Итерация")
plt.ylabel("Изменение Q")
plt.grid()

Тестирование EM-алгоритма на случайных данных.¶

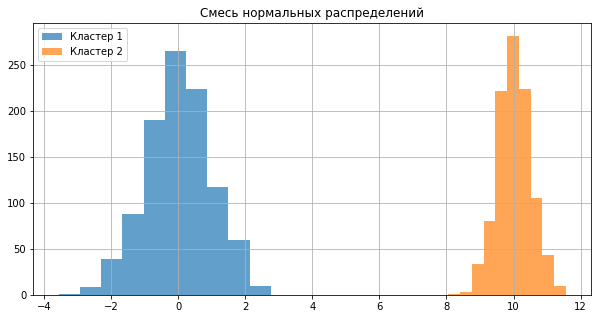
Сильно разрозненные данные.¶

np.random.seed(1234)
x1 = np.random.normal(0, 1, 1000)
x2 = np.random.normal(10, 0.5, 1000)

x = np.hstack((x1, x2))
np.random.shuffle(x)

theta = np.array([np.min(x), (np.max(x) - np.min(x)) / 2, np.max(x), (np.max(x) - np.min(x)) / 2, 1/2])

plt.figure(figsize = (10, 5))
_ = plt.hist(x1, alpha = 0.7, label = 'Кластер 1')
_ = plt.hist(x2, alpha = 0.7, label = 'Кластер 2')
_ = plt.legend()
_ = plt.title("Смесь нормальных распределений")
_ = plt.grid()

theta, Q = EM(x, theta)

theta

array([ 0.01574058,  0.94685783, 10.02088093,  0.24555588,  0.5       ])

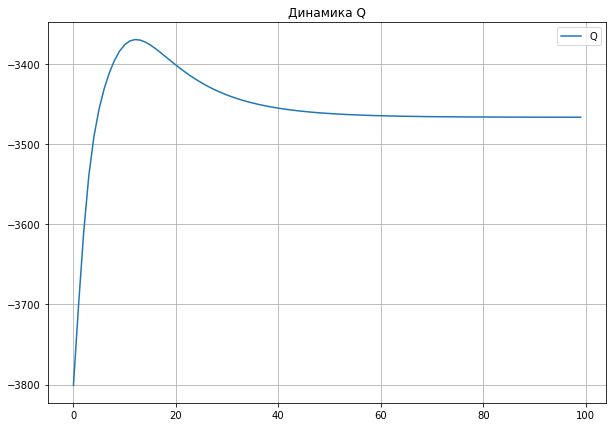
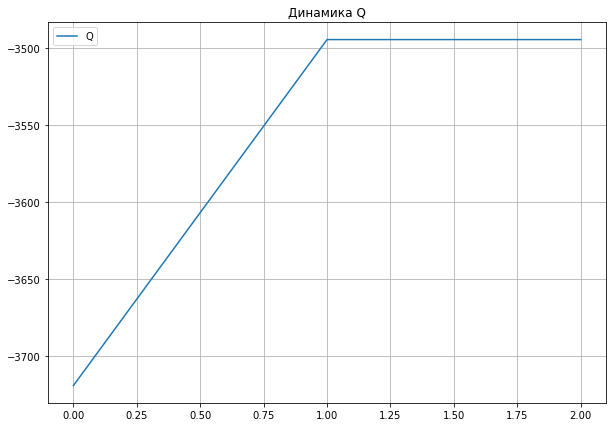
plt.figure(figsize = (10, 7))
_ = plt.plot(Q, label = 'Q')
_ = plt.legend()
_ = plt.grid()
_ = plt.title("Динамика Q")

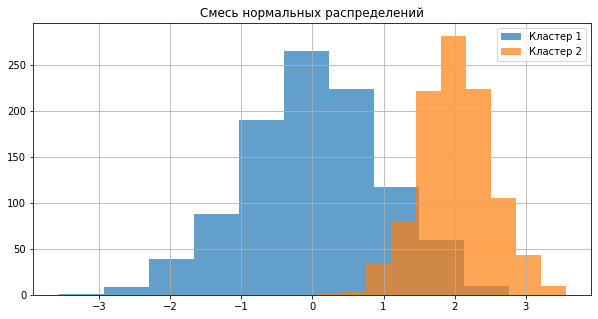
Сильно смешанные данные.¶

np.random.seed(1234)
x1 = np.random.normal(0, 1, 1000)
x2 = np.random.normal(2, 0.5, 1000)

x = np.hstack((x1, x2))
np.random.shuffle(x)

theta = np.array([np.min(x), (np.max(x) - np.min(x)) / 2, np.max(x), (np.max(x) - np.min(x)) / 2, 1/2])

plt.figure(figsize = (10, 5))
_ = plt.hist(x1, alpha = 0.7, label = 'Кластер 1')
_ = plt.hist(x2, alpha = 0.7, label = 'Кластер 2')
_ = plt.legend()
_ = plt.title("Смесь нормальных распределений")
_ = plt.grid()

theta, Q = EM(x, theta)

theta

array([-1.65246121e-03,  9.20790763e-01,  2.02135007e+00,  2.41473450e-01,
        4.95817131e-01])

plt.figure(figsize = (10, 7))
_ = plt.plot(Q, label = 'Q')
_ = plt.legend()
_ = plt.grid()
_ = plt.title("Динамика Q")

Прикладная статистика в машинном обучении

Семинар¶

Постановка задачи.¶

EM-алгоритм в общем виде.¶

Обоснование EM-алгоритма.¶

Обозначения.¶

Пример с лекции: задача о кластеризации (разделение смеси нормальных распределений).¶

Постановка задачи.¶

Определение латентных переменных.¶

E1-шаг.¶

E2-шаг.¶

M-шаг.¶

Решение задачи кластеризации.¶

Динамика Q.¶

Тестирование EM-алгоритма на случайных данных.¶

Сильно разрозненные данные.¶

Сильно смешанные данные.¶