Contents

Лекция

Ограниченные и неограниченные модели

Неограниченная (unrestricted) модель – некоторая модель устройства мира, в истинности которой мы не сомневаемся.

Ограниченная (restricted) модель – модель, которая получается, если в неограниченную модель ввести одно или несколько ограничений на её параметры. В истинности ограниченной модели мы не уверены, и наша цель состоит в том, чтобы статистически протестировать, является ли ограниченная модель также истинной.

Пример

  • неограниченная модель: \(y_i \sim \mathcal{N}(\mu, \sigma^2)\), \(\mathrm{corr}(y_i, y_j) = \rho\), \(i \ne j\).

  • ограниченная модель: \(y_i \sim \mathcal{N}(\mu, \sigma^2)\), \(\mathrm{corr}(y_i, y_j) = 0\), \(i \ne j\).

Статистические тесты, которые используются для проверки истинности ограниченной модели, можно разделить на четыре группы:

  1. LR-тест и похожие на него.

  2. LM-тест и похожие на него.

  3. W-тест и похожие на него.

  4. Экзотика.

Постановка задачи

Предположим, что необходимые условия регулярности на функцию правдоподобия выполнены. Правдоподобие задаётся в стандартном виде:

\[ \ell(y | \theta) = \ln{f(y|\theta}). \]

Разобъём вектор параметров модели \(\theta\) на 2 части:

\[\begin{split} \theta = \begin{pmatrix} \theta_a \\ \theta_b \end{pmatrix}, \end{split}\]

где

\[\begin{split} \theta_a = \begin{pmatrix} \theta_1\\ \vdots\\ \theta_r \end{pmatrix},\text{ } \theta_b = \begin{pmatrix} \theta_{r+1}\\ \vdots\\ \theta_{r+k} \end{pmatrix} \end{split}\]

Для получения ограниченной модели наложим ограничение \(\theta_a = \theta_a^0\). Заметим, что общее число ограничений равно \(r\).

Тест отношения правдоподобия (LR-тест)

Идея: правдоподобие ограниченной и неограниченной моделей не должны сильно различаться.

\[ LR = 2(\max\limits_{\theta_a, \theta_b} \ell(\theta_a, \theta_b) - \max\limits_{\theta_b} \ell(\theta_a^0, \theta_b)). \]

Или в более компактной, но менее формальной форме

\[ LR = 2(\max_{\theta_{UR}} \ell - \max_{\theta_{R}} \ell). \]

Так как ограниченная модель является частным случаем неограниченной, то \(LR\)-статистика всегда неотрицательна. Можно показать, что при верной \(H_0\) и регулярной функции правдоподобия верно, что

\[ LR \xrightarrow{\mathrm{dist}} \chi^2_r, \]

то есть \(LR\)-статистика сходится к хи-квадрат распределению с \(r\) степенями свободы.

Из идеи \(LR\)-статистики следует, что если она получается «большой», то скорее, основная гипотеза неверна. Отсюда

  • Если \(LR > \chi^2_{crit}\), то \(H_0\) отвергается.

  • Если \(LR \leq \chi^2_{crit}\), то \(H_0\) не отвергается.

Пример

В некотором пруду водятся караси, щуки и крокодилы. Вероятность поймать карася - \(\alpha\), щуку - \(\beta\), а крокодила - \((1 - \alpha - \beta)\). Каждый день в течение 100 дней мы ходили на пруд и что-то ловили. В итоге получилось 20 карасей, 60 щук и 20 крокодилов. Проверьте гипотезу

\[ H_0: \beta = 2\alpha \]

против гипотезы

\[ H_A: \beta \ne 2\alpha \]

с помощью \(LR\)-теста.

Решение:

Вычислим логарифм функции правдоподобия \(\ell = \ln \mathbb{P}\)(получить такие данные).

\(\mathbb{P}\)(20 карасей, 60 щук, 20 крокодилов)\(= C \cdot \alpha^{20}\beta^{60}(1-\alpha-\beta)^{20}\), где

\[\begin{split} C = \begin{pmatrix} &100\\ 20 & 60 & 20 \end{pmatrix} = \frac{100!}{20!\cdot60!\cdot20!}. \end{split}\]

Получаем, что \(\ell = \ln C + 20\ln\alpha + 60\ln\beta + 20\ln(1-\alpha-\beta)\) и

\[ LR = 2(\max\limits_{\alpha, \beta} l(\alpha, \beta) - \max\limits_{\beta = 2\alpha} l(\alpha, \beta)). \]

В неограниченной модели мы можем интуитивно оценить \(\alpha\) и \(\beta\) как \(\hat{\alpha} = 0.2\) и \(\hat{\beta} = 0.6\). Те же оценки получатся при честном применении метода максимального правдоподобия. Таким образом мы нашли первый из максимумов - \(\max\limits_{\alpha, \beta} \ell(\alpha, \beta)\) (осталось подставить в \(\ell\) найденные оценки).

Далее с учетом ограничения получаем

\[ \ell (\alpha, \beta)_{\beta = 2\alpha} = \ln C + 20\ln \alpha + 60\ln (2\alpha) + 20 \ln (1-3\alpha), \]
\[ \frac{\partial l}{\partial \alpha} = \frac{80}{\alpha} - \frac{60}{1 - 3\alpha}. \]

Приравниваем производную к нулю и обозначаем за \(\hat{\alpha}^R\) ограниченную оценку параметра \(\alpha\):

\[ 80(1 - 3 \hat{\alpha}^R) = 60 \hat{\alpha}^R \]

Получаем, что \(\hat{\alpha}^R = \frac{4}{15}\), значит \(\hat{\beta}^R = \frac{8}{15}\).

Тогда \(LR\)-статистика равна

\[ LR = 2(20\ln(0.2) + 60\ln(0.6) + 20\ln(0.2) - (20\ln\frac{4}{15} + 60\ln\frac{8}{15} + 20\ln\frac{3}{15})) \approx 2.63 \]

Вспомним, что при верной \(H_0\) \(LR \xrightarrow{\mathrm{dist}} \chi^2_1\) (одно ограничение).

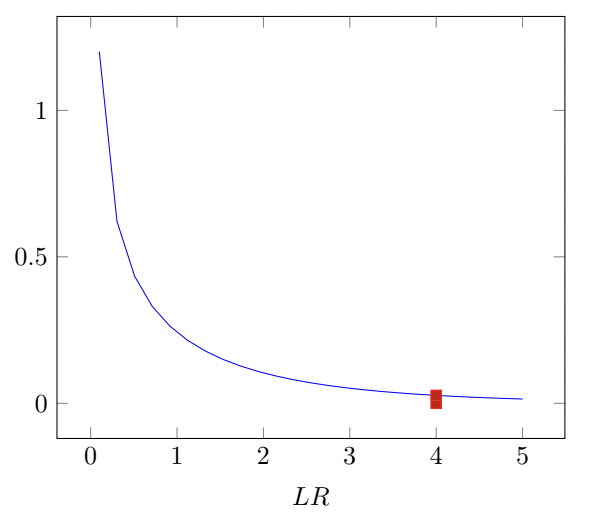
Если мы проверяем гипотезу на уровне значимости 5%, то надо взять \(\chi^2_{crit} \approx 4\) (отмечено на графике ниже). Так как \(LR\) получилось \(\approx 2.63\), то \(H_0\) не отвергается.

../../_images/im1.png

Тест множителей Лагранжа (LM-тест)

Идея: если теневая цена ограничения (равная множителю Лагранжа) слишком велика, то ограничение следует отвергнуть как несоответствующее данным.

Скалярный случай:

\[ LM = \frac{(l'(\theta_0))^2}{Var (l'(\theta_0))} = \frac{l'(\theta_0)^2}{\hat{I}(\theta_0)} \xrightarrow{dist} \chi_1^2 \]

Многомерный случай:

\[ LM = (\left.grad \right |_{(\theta_a = \theta_a^0, \hat{\theta}_b^R)})^T \cdot \hat{I}^{-1} (\theta) \cdot (\left.grad \right |_{(\theta_a = \theta_a^0, \hat{\theta}_b^R)}) \xrightarrow{dist} \chi^2_r \]

Приведём интуицию такого вида статистики. Рассмотрим задачу максимизации правдоподобия с ограничениями:

\[\begin{split} \begin{cases} \ell(y | \theta) \to \max_{\theta}, \\ \theta_a = \theta_a^0 \end{cases} \end{split}\]

Применим метод множителей Лагранжа. Выпишем лагранжиан и найдём его производные:

\[ \mathcal{L} (\theta_a, \theta_b, \lambda) = \ell(y|\theta_a, \theta_b) + \lambda \cdot (\theta_a - \theta_a^0). \]
\[\begin{split} \begin{cases} \frac{\partial \mathcal{L}}{\partial \theta_a} = \frac{\partial \ell}{\partial \theta_a} + \lambda = 0\\ \frac{\partial \mathcal{L}}{\partial \theta_b} = \frac{\partial \ell}{\partial \theta_b} = 0\\ \frac{\partial \mathcal{L}}{\partial \lambda} = \theta_a - \theta_a^0 = 0 \end{cases} \end{split}\]

Из первого уравнения получаем \(\hat{\lambda} = -\frac{\partial l}{\partial \theta_a}\). Это условие показывает один из дополнительных смыслов первой производной логарифма функции правдоподобия - она также является множителем Лагранжа. В соответствии с идеей метода, нам нужно протестировать величину первой производной логарифма правдоподобия. LM-cтатистика получается в предположении о том, что для первой производной логарифма правдоподобия выполняется ЦПТ, поэтому её центрированный и нормированный квадрат будет иметь хи-квадрат распределение.

Тест Вальда (W-тест)

Идея: \(\theta_0\) не должна быть слишком далека от \(\hat{\theta}\).

Скалярный случай:

\[ W = \frac{(\hat{\theta}_a - \theta_0)^2}{\hat{Var}(\hat{\theta}_a)} \xrightarrow{dist} \chi_1^2 \]

Многомерный случай:

\[ W = (\hat{\theta}_a - \theta_0)^{T}\hat{Var}^{-1}(\hat{\theta}_a)(\hat{\theta}_a - \theta_0) \xrightarrow{dist} \chi_r^2 \]

Необходимую дисперсию можно найти при помощи информации Фишера:

\[\begin{split} \begin{pmatrix} \hat{Var}(\hat{\theta}_a) & \hat{Cov}(\hat{\theta}_a, \hat{\theta}_b)\\ \hat{Cov}(\hat{\theta}_a, \hat{\theta}_b) & \hat{Var}(\hat{\theta}_b) \end{pmatrix} = I^{-1}(\hat{\theta}) \end{split}\]

Продолжение примера про пруд

Протестируем сформулированную гипотезу при помощи теста Вальда. Для удобства, чтобы \(\hat{\theta}_0\) равнялось 0 заменим наши \(\theta\) следующим образом:

\[\begin{split} \theta_a = 2 \alpha - \beta = 2 \cdot 0.2 - 0.6 = -0.2\\ \end{split}\]
\[ \theta_b = \beta \]

Чтобы найти информацию Фишера, нам понадобятся вторые производные логарифма правдоподобия.

\[ l'_\alpha = \frac{y_{кар}}{\alpha} - \frac{y_{крок}}{1-\alpha-\beta} \]
\[ l''_{\alpha\alpha} = -\frac{y_{кар}}{\alpha^2} - \frac{y_{крок}}{(1-\alpha-\beta)^2} \]
\[\begin{split} -H = \begin{pmatrix} \frac{y_{кар}}{\alpha^2} + \frac{y_{крок}}{(1-\alpha-\beta)^2} & \frac{y_{крок}}{(1-\alpha-\beta)^2} \\ \frac{y_{крок}}{(1-\alpha-\beta)^2} & \frac{y_{щук}}{\alpha^2} + \frac{y_{крок}}{(1-\alpha-\beta)^2} \end{pmatrix} \end{split}\]
\[\begin{split} I=E(-H)= \begin{pmatrix} \frac{n\alpha}{\alpha^2} + \frac{n(1-\alpha-\beta)}{(1-\alpha-\beta)^2} & \frac{n(1-\alpha-\beta)}{(1-\alpha-\beta)^2} \\ \frac{n(1-\alpha-\beta)}{(1-\alpha-\beta)^2} & \frac{n\beta}{\beta^2} + \frac{n(1-\alpha-\beta)}{(1-\alpha-\beta)^2} \end{pmatrix} = n \begin{pmatrix} \frac{1}{\alpha} + \frac{1}{1-\alpha-\beta} & \frac{1}{1-\alpha-\beta} \\ \frac{1}{1-\alpha-\beta} & \frac{1}{\beta} + \frac{1}{1-\alpha-\beta} \end{pmatrix} \end{split}\]
\[\begin{split} \hat{I} = 100 \begin{pmatrix} 10 & 5 \\ 5 & \frac{5}{3} + 5 \end{pmatrix} \end{split}\]
\[\begin{split} \hat{I}^{-1} = \hat{Var}(\hat{\theta}) = \frac{1}{100} \cdot \frac{1}{\frac{100}{3} - 25} \begin{pmatrix} \frac{5}{3} + 5 & -5 \\ -5 & 10 \end{pmatrix} = \frac{1}{100} \cdot \frac{3}{125} \begin{pmatrix} \frac{20}{3} & -5 \\ -5 & 10 \end{pmatrix} = \begin{pmatrix} \frac{1}{625} & \frac{-3}{2500} \\ \frac{-3}{2500} & \frac{3}{1250} \end{pmatrix} = \begin{pmatrix} \hat{Var}(\hat{\alpha}) & \hat{Cov}(\hat{\alpha}, \hat{\beta}) \\ \hat{Cov}(\hat{\alpha}, \hat{\beta}) & \hat{Var}(\hat{\beta}) \end{pmatrix} \end{split}\]

Теперь из этой матрицы достаем нужную нам \(\hat{Var}(\hat{\theta}_a) = \hat{Var}(2\hat{\alpha} - \hat{\beta}) = 4\hat{Var}(\hat{\alpha}) + \hat{Var}(\hat{\beta}) - 2 \cdot 2 \hat{Cov}(\hat{\alpha}, \hat{\beta})=\frac{0.2^2}{\frac{4}{625} + \frac{3}{1250} + \frac{12}{2500}} \approx 2.94.\)

Аналогично \(LR\) тесту сравниваем \(\chi_{crit}^2 \approx 4\) c получившимся значением статистики Вальда. \(H_0\) не отвергается, так как \(2.94 < 4\).

Геометрический смысл тестов

На рисунке ниже представлен геометрический смысл тестов.

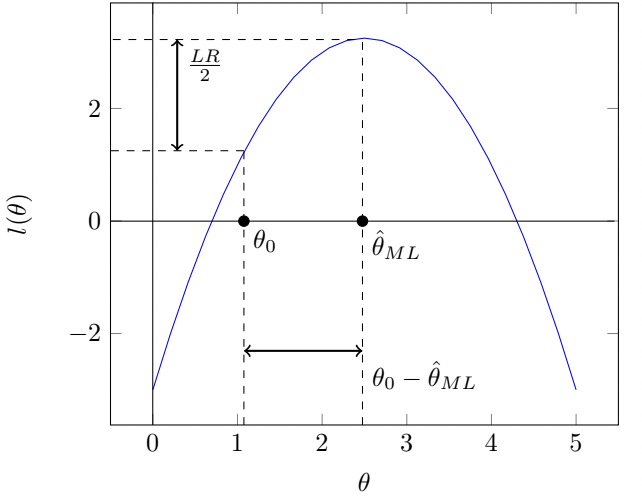
../../_images/im2.png

Геометрический смысл \(LR\)-теста следует из определения: он измеряет разницу между значениями логарифма правдоподобия в R-точке и UR-точке (вдоль вертикальной оси). Теста Вальда измеряет эту разницу между значениями оценок в R-точке и UR-точке (вдоль горизонтальной оси). \(LM\)-тест измеряет разницу в наклонах касательных, проведённых в в R-точке и UR-точке (равен 0).

Дополнительные материалы

Благодарности

  • Гришанин Виктор

  • Малафеев Михаил

  • Богданов Игорь

Семинар Семинар